CD reflecting rainbow colours: So almost all of you have seen a rainbow formation on rainy days. Every one of us knows what diffraction is. It is the bending of light around the corner of an obstacle. Reflected light produces fridges of light, dark or colored bands. At times diffraction of sunlight in clouds produces a multitude of colors.

In his 1704 treatise on the theory of optical phenomena (Opticks), Sir Isaac Newton wrote that 'light is never known to follow crooked passages nor to bend into the shadow'. He explained this observation by describing how particles of light always travel in straight lines, and how objects positioned within the path of light particles would cast a shadow because the particles could not spread out behind the object. Depending on the circumstances that give rise to the phenomenon, diffraction can be perceived in a variety of different ways. Scientists have cleverly utilized diffraction of neutrons and X-rays to elucidate the arrangement of atoms in small ionic crystals, molecules, and even such large macromolecular assemblies as proteins and nucleic acids. Electron diffraction is often employed to examine periodic features of viruses, membranes, and other biological organisms, as well as synthetic and naturally occurring materials. No lens exists that will focus neutrons and X-rays into an image, so investigators must reconstruct images of molecules and proteins from the diffraction patterns using sophisticated mathematical analysis. Fortunately, magnetic lenses can focus diffracted electrons in the electron microscope, and glass lenses are very useful for focusing diffracted light to form an optical image that can easily be viewed.

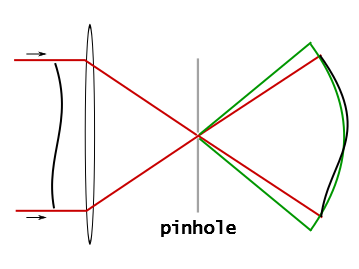
Introduction to Diffraction - When we view a specimen, whether directly or with a microscope, telescope, or other optical instrument, the image we see is composed of a myriad of overlapping points of light emanating from the plane of the specimen. Therefore, the appearance and integrity of the image from a single point of light holds a significant amount of importance with regards to formation of the overall image. Because the image-forming light rays are diffracted, a single point of light is never really seen as a point in the microscope, but rather as a diffraction pattern containing a central disk or spot of light having a finite diameter and encircled by a fading series of rings. As a result, the image of a specimen is never an exact representation of the specimen, and a lower limit is imposed on the smallest detail in the specimen that can be resolved. The resolving power is the ability of an optical instrument to produce clearly separated images of two adjacent points. Up to the point at which diffraction causes the resolution to be limited, the quality of the lenses and mirrors in the instrument, as well as the properties of the surrounding medium (usually air), determine the final resolution.

Sir George Biddell Airy (1801-1892) - Sir George Airy was a distinguished nineteenth century English Astronomer Royal who carried out optical research and first drew attention to the visual defect of astigmatism. Airy manufactured the first correcting eyeglasses (1825) using a cylindrical lens design that is still in use. The diffraction disks that bear his name (Airy Disks) were discovered in the spherical center of a wavefront traveling through a circular aperture. These diffraction patterns form the smallest unit that comprises an image, thus determining the limits of optical resolution.

Jacques Babinet (1794-1872) - Jacques Babinet was a French physicist, mathematician, and astronomer born in Lusignan, who is most famous for his contributions to optics. Among Babinet's accomplishments are the 1827 standardization of the Ångström unit for measuring light using the red cadmium line's wavelength, and the principle (bearing his name) that similar diffraction patterns are produced by two complementary screens.

William Henry Bragg (1862-1942) - Sir William Henry Bragg was a noted British physicist and President of the Royal Society who had numerous research interests, but the work that earned him a rank as one the great leaders in science was his historic advancements in X-ray crystallography. Working with his son William Lawrence Bragg, he developed a method of bombarding single crystals with high-energy X-rays emitted by specially constructed vacuum tubes. By examining the pattern of X-rays diffracted by various crystals, Bragg and his son were able to establish some fundamental mathematical relationships between an atomic crystal structure and its diffraction pattern. For this achievement, William Henry Bragg and William Lawrence Bragg were awarded the Nobel Prize in Physics in 1915.

Augustin-Jean Fresnel (1788-1827) - Augustin-Jean Fresnel, was a nineteenth century French physicist, who is best known for the invention of unique compound lenses designed to produce parallel beams of light, which are still used widely in lighthouses. In the field of optics, Fresnel derived formulas to explain reflection, diffraction, interference, refraction, double refraction, and the polarization of light reflected from a transparent substance.

Lord Rayleigh (John William Strutt) - (1842-1919) - Lord Rayleigh was a British physicist and mathematician who worked in many disciplines including electromagnetics, physical optics, and sound wave theory. The criteria he defined still act as the limits of resolution of a diffraction-limited optical instrument. Rayleigh wrote over 446 scientific papers, but is perhaps best known for his discovery of the inert gas argon, which earned him a Nobel Prize.

Diffraction of Light - Several of the classical and most fundamental experiments that help explain diffraction of light were first conducted between the late seventeenth and early nineteenth centuries by Italian scientist Francesco Grimaldi, French scientist Augustin Fresnel, English physicist Thomas Young, and several other investigators. These experiments involve propagation of light waves though a very small slit (aperture), and demonstrate that when light passes through the slit, the physical size of the slit determines how the slit interacts with the light. This interactive tutorial explores the diffraction of a monochromatic light beam through a slit of variable aperture.

Particle Size and Diffraction Angles - The phenomenon of diffraction is observed when a specimen consisting of fine particles is illuminated with a beam of semi-coherent, collimated light. Good examples of this effect are a microscope slide containing particles of various sizes, and the spreading of automobile headlights on a foggy night. In both cases, diffraction is manifested through the scattering of light by small particles having linear physical dimensions similar to the wavelength of the illumination. This interactive tutorial demonstrates the effects of diffraction at an aperture and explores the spreading of light by a specimen composed of individual particles.

Line Spacing Calculations from Diffraction Gratings - By definition, a diffraction grating is composed of a planar substrate containing a parallel series of linear grooves or rulings, which can be transparent, semi-transparent, or opaque. When the spacing between lines on a diffraction grating is similar in size to the wavelength of light, an incident collimated and coherent light beam will be strongly diffracted upon encountering the grating. This interactive tutorial examines the effects of wavelength on the diffraction patterns produced by a virtual periodic line grating of fixed line spacing.

Light Diffraction Through a Periodic Grating - A model for the diffraction of visible light through a periodic grating is an excellent tool with which to address both the theoretical and practical aspects of image formation in optical microscopy. Light passing through the grating is diffracted according to the wavelength of the incident light beam and the periodicity of the line grating. This interactive tutorial explores the mechanics of periodic diffraction gratings when used to interpret the Abbe theory of image formation in the optical microscope.

Airy Pattern Formation - When an image is formed in the focused image plane of an optical microscope, every point in the specimen is represented by an Airy diffraction pattern having a finite spread. This occurs because light waves emitted from a point source are not focused into an infinitely small point by the objective, but converge together and interfere near the intermediate image plane to produce a three-dimensional Fraunhofer diffraction pattern. This interactive tutorial explores the origin of Airy diffraction patterns formed by the rear aperture of the microscope objective and observed at the intermediate image plane.

Airy Pattern Basics - The three-dimensional diffraction pattern formed by a circular aperture near the focal point in a well-corrected microscope is symmetrically periodic along the axis of the microscope as well as radially around the axis. When this diffraction pattern is sectioned in the focal plane, it is observed as the classical two-dimensional diffraction spectrum known as the Airy pattern. This tutorial explores how Airy pattern size changes with objective numerical aperture and the wavelength of illumination; it also simulates the close approach of two Airy patterns.

Numerical Aperture and Image Resolution - The Airy pattern formed at the microscope intermediate image plane is a three-dimensional diffraction image, which is symmetrically periodic both along the optical axis of the microscope, and radially across the image plane. This diffraction pattern can be sectioned in the focal plane to produce a two-dimensional diffraction pattern having a bright circular disk surrounded by an alternating series of bright and dark higher-order diffraction rings whose intensity decreases as they become further removed from the central disk. Usually only two or three of the circular luminous rings are visible in the microscope (this number is dependent upon the objective numerical aperture), because the higher orders are absorbed by stray light and are not visible.

Conoscopic Images of Periodic Gratings - The purpose of this tutorial is to explore the reciprocal relationship between line spacings in a periodic grid (simulating a specimen) and the separation of the conoscopic image at the objective aperture plane. When the line grating has broad periodic spacings, several images of the condenser iris aperture appear in the objective rear focal plane. If white light is used to illuminate the line grating, higher order diffracted images of the aperture appear with a blue fringe closer to the zeroth order (central) image and with a green-yellow-red spectrum appearing further out towards the objective aperture periphery.

Spatial Frequency and Image Resolution - When a line grating is imaged in the microscope, a series of conoscopic images representing the condenser iris opening can be seen at the objective rear focal plane. This tutorial explores the relationship between the distance separating these iris opening images and the periodic spacing (spatial frequency) of lines in the grating.

Airy Patterns and the Rayleigh Criterion - Airy diffraction pattern sizes and their corresponding radial intensity distribution functions are sensitive to both objective numerical aperture and the wavelength of illuminating light. For a well-corrected objective with a uniform circular aperture, two adjacent points are just resolved when the centers of their Airy patterns are separated by a distance r. This tutorial examines how Airy disk sizes, at the limit of optical resolution, vary with changes in objective numerical aperture and illumination wavelength and how these changes affect the resolution of the objective.

Periodic Diffraction Images - When a microscope objective forms a diffraction-limited image of an object, it produces a three-dimensional diffraction pattern that is periodic both along the optical axis and laterally within the intermediate image plane. This tutorial explores diffraction images produced by a periodic object at several focal depths.

Reference Listing - The reference materials listed in this section are an excellent source of additional information on the diverse topic of light diffraction and scattering by gratings and through apertures. Included are references to books, book chapters, and review articles, which discuss the theory and applications of these diverse topics, and how they relate to the physics of light and color.

Contributing Authors

Douglas B. Murphy - Department of Cell Biology and Microscope Facility, Johns Hopkins University School of Medicine, 725 N. Wolfe Street, 107 WBSB, Baltimore, Maryland 21205.

Kenneth R. Spring - Scientific Consultant, Lusby, Maryland, 20657.

Matthew Parry-Hill, Thomas J. Fellers, and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.

Learning Objectives

By the end of this section, you will be able to:

• Explain the phenomenon of diffraction and the conditions under which it is observed
• Describe diffraction through a single slit

After passing through a narrow aperture (opening), a wave propagating in a specific direction tends to spread out. For example, sound waves that enter a room through an open door can be heard even if the listener is in a part of the room where the geometry of ray propagation dictates that there should only be silence. Similarly, ocean waves passing through an opening in a breakwater can spread throughout the bay inside. (Figure (PageIndex{1})). The spreading and bending of sound and ocean waves are two examples of diffraction, which is the bending of a wave around the edges of an opening or an obstacle—a phenomenon exhibited by all types of waves.

The diffraction of sound waves is apparent to us because wavelengths in the audible region are approximately the same size as the objects they encounter, a condition that must be satisfied if diffraction effects are to be observed easily. Since the wavelengths of visible light range from approximately 390 to 770 nm, most objects do not diffract light significantly. However, situations do occur in which apertures are small enough that the diffraction of light is observable. For example, if you place your middle and index fingers close together and look through the opening at a light bulb, you can see a rather clear diffraction pattern, consisting of light and dark lines running parallel to your fingers.

Diffraction through a Single Slit

Diffraction Of Light

Light passing through a single slit forms a diffraction pattern somewhat different from those formed by double slits or diffraction gratings, which we discussed in the chapter on interference. Figure (PageIndex{2}) shows a single-slit diffraction pattern. Note that the central maximum is larger than maxima on either side and that the intensity decreases rapidly on either side. In contrast, a diffraction grating produces evenly spaced lines that dim slowly on either side of the center.

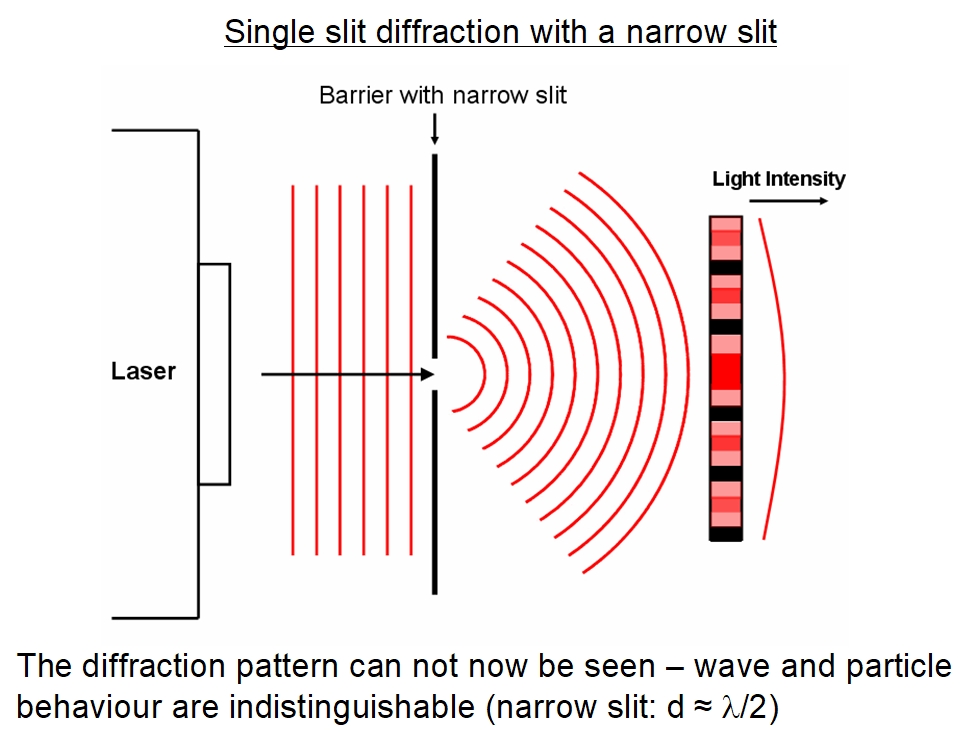
The analysis of single-slit diffraction is illustrated in Figure (PageIndex{2}). Here, the light arrives at the slit, illuminating it uniformly and is in phase across its width. We then consider light propagating onwards from different parts of the same slit. According to Huygens’s principle, every part of the wave front in the slit emits wavelets, as we discussed in The Nature of Light. These are like rays that start out in phase and head in all directions. (Each ray is perpendicular to the wave front of a wavelet.) Assuming the screen is very far away compared with the size of the slit, rays heading toward a common destination are nearly parallel. When they travel straight ahead, as in part (a) of the figure, they remain in phase, and we observe a central maximum. However, when rays travel at an angle θ relative to the original direction of the beam, each ray travels a different distance to a common location, and they can arrive in or out of phase. In part (b), the ray from the bottom travels a distance of one wavelength λ farther than the ray from the top. Thus, a ray from the center travels a distance λ/2 less than the one at the bottom edge of the slit, arrives out of phase, and interferes destructively. A ray from slightly above the center and one from slightly above the bottom also cancel one another. In fact, each ray from the slit interferes destructively with another ray. In other words, a pair-wise cancellation of all rays results in a dark minimum in intensity at this angle. By symmetry, another minimum occurs at the same angle to the right of the incident direction (toward the bottom of the figure) of the light.

At the larger angle shown in part (c), the path lengths differ by (3λ/2) for rays from the top and bottom of the slit. One ray travels a distance (λ) different from the ray from the bottom and arrives in phase, interfering constructively. Two rays, each from slightly above those two, also add constructively. Most rays from the slit have another ray to interfere with constructively, and a maximum in intensity occurs at this angle. However, not all rays interfere constructively for this situation, so the maximum is not as intense as the central maximum. Finally, in part (d), the angle shown is large enough to produce a second minimum. As seen in the figure, the difference in path length for rays from either side of the slit is (a sin theta), and we see that a destructive minimum is obtained when this distance is an integral multiple of the wavelength.

Thus, to obtain destructive interference for a single slit,

[underbrace{a sin θ = mλ}_{text{destructive interference}}]

where

• (m = ±1, ±2, ±3,...),
• (a) is the slit width,
• (λ) is the light’s wavelength,
• (θ) is the angle relative to the original direction of the light, and
• (m) is the order of the minimum.

Figure (PageIndex{3}) shows a graph of intensity for single-slit interference, and it is apparent that the maxima on either side of the central maximum are much less intense and not as wide. This effect is explored in Double-Slit Diffraction.

Example (PageIndex{1}): Calculating Single-Slit Diffraction

Visible light of wavelength 550 nm falls on a single slit and produces its second diffraction minimum at an angle of 45.0° relative to the incident direction of the light, as in Figure (PageIndex{5}).

1. What is the width of the slit?
2. At what angle is the first minimum produced?

Strategy

From the given information, and assuming the screen is far away from the slit, we can use the equation (a sin θ = mλ) first to find (a), and again to find the angle for the first minimum (theta_1).

Solution

1. We are given that (λ=550,nm), (m=2), and (theta_2 = 45.0°). Solving the equation (a , sin , theta = mlambda) for (a) and substituting known values gives

   [a = frac{mlambda}{sin , theta_2} = frac{2(550 , nm)}{sin , 45.0°} = frac{1100 times 10^{-9} m}{0.707} = 1.56 times 10^{-6} m. nonumber]

2. Solving the equation (a , sin , theta = mlambda) for (sin , theta_1) and substituting the known values gives

   [sin , theta_1 = frac{mlambda}{a} = frac{1(550 times 10^{-9}m)}{1.56 times 10^{-6}m}. nonumber]

   Thus the angle (theta_1) is

   [theta_1 = sin^{-1}0.354 = 20.7°. nonumber]

Significance

We see that the slit is narrow (it is only a few times greater than the wavelength of light). This is consistent with the fact that light must interact with an object comparable in size to its wavelength in order to exhibit significant wave effects such as this single-slit diffraction pattern. We also see that the central maximum extends 20.7° on either side of the original beam, for a width of about 41°. The angle between the first and second minima is only about 24°(45.0°−20.7°). Thus, the second maximum is only about half as wide as the central maximum.

Exercise (PageIndex{1})

Diffraction Wave

Suppose the slit width in Example (PageIndex{1}) is increased to (1.8 times 10^{-6} m). What are the new angular positions for the first, second, and third minima? Would a fourth minimum exist?

(17.8^o), (37.7^o), (66.4^o); no

Contributors and Attributions

Diffraction Wave

• Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).